|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||||||||
|
Lineare Funktionen haben allgemein die Form y = m·x + t. Bisher haben wir den Spezialfall untersucht, bei dem t = 0 ist. Diese Funktionen ergaben Ursprungsgeraden mit der Steigung m.
Was ändert sich nun an den Geraden, wenn noch ein fester Wert t hinzu addiert wird? |
 |
|||||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Beispiele für allgemeine lineare Funktionen | ||||||||||||||||||||||||||||||||
|
Allgemeine lineare Funktionen y = m·x + t ergeben sich aus den Funktionen y = m·x, wenn man noch eine feste Zahl t hinzu addiert.
y = 2x + 1 y = -0,5x + 3 y = 1,2x – 0,7 y =
|

|
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Wertetabelle und Graph | ||||||||||||||||||||||||||||||||
|
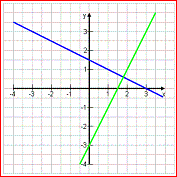
Wie unterscheidet sich nun die Gerade y = m·x + t von der Geraden y = m·x, die wir bereits kennen?
Schauen wir uns die Beispiele y = 0,5·x und y = 0,5·x + 2 an. 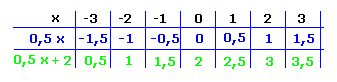
|
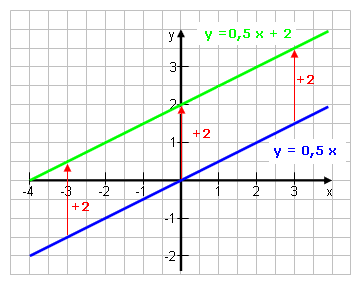
Funktionen der Form
y = m·x + t sind um t nach oben verschoben. |
|||||||||||||||||||||||||||||||
|
Bereits in der Wertetabelle erkennt man, dass auf jeden y-Wert von y = 0,5·x noch die 2 addiert wird. Die ganze Funktion wird also um 2 nach oben verschoben.
An den Geraden sieht man es noch deutlicher: Im Vergleich zu y = 0,5·x ist y = 0,5·x + 2 um 2 nach oben verschoben. Die Steigung m hat sich hingegen nicht verändert! Sie ist bei beiden Geraden 0,5. |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
| Steigung und y-Achsenabschnitt | ||||||||||||||||||||||||||||||||
|
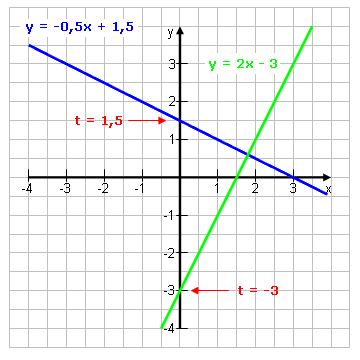
Steigung m:
Die Steigung m gibt immer noch an, um wie viel die Funktion steigt oder fällt, wenn man x um 1 erhöht, also um 1 nach rechts geht. y-Achsenabschnitt t: t gibt an, um wie viel die Gerade gegenüber der Ursprungsgeraden nach oben oder unten verschoben ist. Sie verläuft dadurch nicht mehr durch den Ursprung (0|0) sondern schneidet die y-Achse bei t. Man nennt t deshalb den y-Achsenabschnitt.
y = m·x + t
|
|
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Funktionen der Form y = m·x + t zeichnen | ||||||||||||||||||||||||||||||||
|
Im vorherigen Kapitel sind wir immer vom Ursprung ausgegangen. Das müssen wir nun ändern, da unsere Funktionen in der Regel nicht mehr durch diesen verlaufen.
So zeichnest du eine lineare Funktion: Du beginnst bei dem Schnittpunkt mit der y-Achse. Das ist einfach bei t auf der y-Achse. Als Punkt formuliert: Sy(0|t). Dann wie bisher: 1 nach rechts und die Steigung m nach oben oder unten. |

|
|||||||||||||||||||||||||||||||
|
Beispiele:
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Spezialfälle | ||||||||||||||||||||||||||||||||
|
Anhand der Funktionsgleichung kann man nun direkt beurteilen, wie eine Gerade verläuft. Man braucht sie nicht einmal zu zeichnen:
y = -2x + 4 Schneidet die y-Achse bei +4 und läuft dann recht steil mit der Steigung -2 nach unten. y = 5x (y = 5·x + 0) Ursprungsgerade (durch (0|0)), die steil mit der Steigung 5 nach oben läuft. y = 7 (y = 0·x + 7) Waagerechte Gerade (m = 0), die die y-Achse bei 7 schneidet. Eine "konstante" Funktion. y = 0 Die x-Achse. |
|
|||||||||||||||||||||||||||||||
|
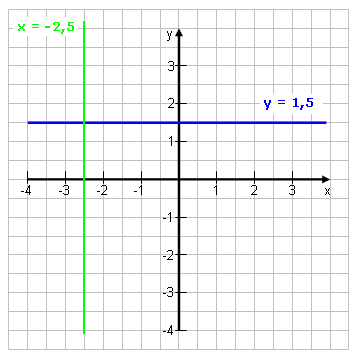
Die y-Achse wird stattdessen durch x = 0 beschrieben.
Allerdings ist das dann keine Funktion mehr, weil zu x = 0 unendlich viele y-Werte gehören. Es ist nur noch eine Relation. Überhaupt kann man senkrechte Geraden einfach über ihre x-Position angeben:
|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
| Die Punkt-Steigungs-Form | ||||||||||||||||||||||||||||||||
|
Die allgemeine Form einer linearen Funktion ist:
y = m·x + t Es ist aber auch möglich, die Funktionen in der folgenden Form anzugeben, der Punkt-Steigungs-Form: y = m·(x – xP) + yP |
Punkt-Steigungs-Form
y = m·(x – xP) + yP y = 2·(x – 1) + 5 
Um ehrlich zu sein: Für Geraden lohnt sich diese Form überhaupt nicht! Sie wird eigentlich erst in der 10. Klasse interessant, wenn es um Parabeln geht!!!
|
|||||||||||||||||||||||||||||||
|
Statt y = 2·x + 3 ergäbe sich: y = 2·(x – 1) + 5
Dass es sich um dieselbe Funktion handelt, sieht man leicht, wenn man die Klammer wieder auflöst: y = 2·(x – 1) + 5 = 2·x – 2·1 + 5 = 2·x + 3 |
||||||||||||||||||||||||||||||||
|
Die Punkt-Steigungs-Form hat zwei Nachteile:
1. Sie sieht komplizierter aus. 2. Man erkennt den y-Achsen-Abschnitt nicht Aber sie hat auch einen Vorteil: Man erkennt sofort einen Punkt durch den sie läuft. Hier ist es der Punkt P(1|5). Die x-Koordinate des Punktes steht also in der Klammer mit falschem Vorzeichen, die y-Koordinate des Punktes hinter der Klammer mit richtigem Vorzeichen. Deshalb steht in der Formel auch – xP und + yP. |
||||||||||||||||||||||||||||||||
|
Die Punkt-Steigungs-Form ist nützlich, wenn man nicht gleich die Funktionsgleichung geliefert bekommt, sondern nur die Steigung und einen Punkt, durch den die Gerade läuft. Dann setzt man beides ein und hat sofort die Gleichung. (Machen wir im nächsten Kapitel!)
|
||||||||||||||||||||||||||||||||